Lógica matemática v.s. estadística bayesiana

El Lenguaje Natural es poderoso y sin lugar a dudas bello, gracias a sus sofisticadas y sutiles reglas los artistas tienen un sinfín de posibilidades en prosa y en verso. Desafortunadamente existen instancias en las que el lenguaje natural no es la mejor manera de comunicarnos, pensemos por ejemplo en la paradoja de Russell:
Si un científico de datos A revisa el código de todos los científicos de datos que no revisan su código, ¿quién revisa el código de A?
Con arduo trabajo los matemáticos han postulado sistemas axiomáticos en los cuales este tipo de ambigüedades no son posibles, para hacerlo se han tenido que enfrentar a resultados nada intuitivos como los Teoremas de Incompletitud de Gödel sobre los cuales hemos hablado anteriormente en este mismo boletín. En buena medida la creación de las computadoras y su enorme fiabilidad es gracias al uso de un lenguaje formal como Python para programar sus razonamientos.

En este texto hablaremos sobre cómo la comprensión cabal de la estadística y la probabilidad bayesiana puede ser utilizada por los científicos de datos y los analistas cuantitativos para mejorar su comunicación sobre las deducciones que extraen de sus bases de datos.
Marketing digital meets data science
Así como los matemáticos y computólogos utilizan un lenguaje formal para realizar sus razonamientos, podríamos argumentar que los científicos de datos y los analistas cuantitativos se apoyan de la estadística para comprender fenómenos complejos y prevenir falacias o paradojas.
Pensemos en el ejemplo sencillo de la correlación, es razonable imaginar que si aumenta el tráfico de interacciones en la red social de una compañía, también aumentarán sus ventas, sin embargo esto solo es una intuición y para sostener una afirmación semejante es necesario basarnos en los datos.

A partir de ahora supondremos que tenemos a nuestro alcance una base de datos con dos columnas X e Y que registran el número de interacciones y ventas diariamente, con el fin de simplificar el problema obviaremos los fenómenos temporales que podrían influir en esta base de datos. Un enfoque obvio sería calcular la correlación entre estas dos columnas, sabemos que si esta métrica es cercana a uno entonces es bastante probable que la siguiente afirmación sea cierta:
Si las interacciones en las redes sociales aumentan, entonces las ventas también lo harán.
A partir de ahora vamos a estudiar a la afirmación anterior desde el punto de vista de la lógica clásica, comenzaremos con la lógica proposicional. A partir de ahí explicaremos cómo el teorema de Bayes modifica sustancialmente el punto de vista de la lógica clásica y por lo tanto esto deberá influir en las conclusiones de los científicos de datos.
Condicional material clásica y la correlación
Desde el punto de vista de la lógica clásica, la condicional es una afirmación que podría o no ser cierta, normalmente se escribirá de la siguiente manera a la condicional:
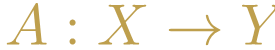
Desde el punto de vista de la lógica proposicional, esta nueva afirmación a la que llamaremos A es cierta en todos los casos siguientes:
- Cuando el tráfico aumente y las ventas también aumenten.
- Cuando el tráfico no aumente y las ventas aumenten.
- Cuando el tráfico no aumente y las ventas tampoco aumenten.
Tanto el primero como el tercer caso corresponden con la definición matemática de la correlación de Pearsson sin embargo el segundo caso es un poco extraño (especialmente si suponemos la ley del tercero excluido) e intuitivamente no corresponde con la correlación positiva entre dos variables, esto significa que la siguiente manera de expresar la afirmación A no podría ser equivalente:
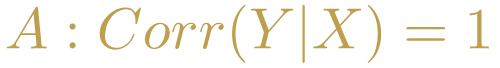
Quienes comprendan correctamente el concepto de correlación, notarán que el segundo caso sí corresponde con el caso de una correlación cercana a -1 y por ello estaríamos muy tentados a tratar de escribir a la afirmación A de la siguiente manera:
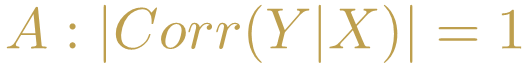
Desafortunadamente esto nuevamente nos trae problemas pues el enunciado original de implicación es falso cuando el tráfico no aumenta y las ventas sí y este nuevo enunciado sería cierto en este caso.
- EJERCICIO: Quienes deseen asegurarse del razonamiento anterior los invitamos a que calculen las tablas de verdad de las siguientes afirmaciones para cerciorarse, desde mi punto de vista es un ejercicio muy divertido.

Tomando en cuenta lo anterior ya podemos intuir que los razonamientos de la lógica proposicional no son necesariamente útiles en ciencia de datos. Los científicos de datos saben que existen otros métodos para relacionar estadísticamente a dos variables, por ejemplo podemos pensar en la probabilidad condicional sobre la cual hablaremos ahora.
Condicional material y probabilidad condicional
Utilizando la probabilidad condicional es posible escribir la primera afirmación A (la condición material) de la siguiente manera:
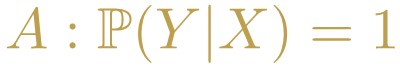
- EJERCICIO: Si la probabilidad de Y condicionada a X fuera igual a cero, entonces esta afirmación ¿a cuál enunciado de la lógica proposicional es equivalente?
La probabilidad condicional nos permite realizar afirmaciones más complicadas como la siguiente:
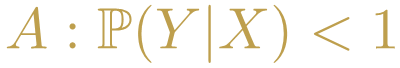
En este caso estamos diciendo que en algunas ocasiones el aumento en el flujo en una red social aumentan las ventas y en otras ocasiones no es cierto, lamentablemente esta afirmación no es demasiado útil para un negocio. Probemos mejor con la siguiente:

En este caso estamos diciendo que las ventas aumentan más frecuentemente cuando sé que hay un alto flujo en las redes sociales lo cual suena parecido a una afirmación interesante para nuestro negocio.
Teorema de Bayes
Para concluir vamos a enunciar una consecuencia inmediata del teorema de Bayes la cual es bastante interesante:
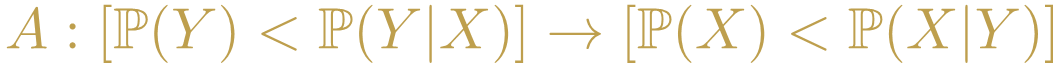
- EJERCICIO: Utilizar el teorema de bayes para demostrar que la afirmación A siempre es cierta.
Esta afirmación nos está diciendo lo siguiente:
Siempre que el número de ventas aumente al saber que han aumentado las interacciones en una red social, entonces el número de interacciones en una red social aumentarán al saber que han aumentado el número de ventas.
Desde mi punto de vista es muy útil para los científicos de datos saber que lo anterior es cierto independientemente de quiénes sean las variables aleatorias X e Y pues esto puede ayudarles a explicar mejor los resultados de sus análisis.
¿Dónde aprender más sobre Ciencia de Datos y Matemáticas?
Quienes deseen aprender sobre IA y sus aplicaciones los invitamos a conocer los temarios de nuestros cursos.
- Track de Ciencia de Datos. (49 semanas).
- Machine Learning & AI for the Working Analyst ( 12 semanas).
- Matemáticas para Ciencia de Datos ( 24 semanas).
- Especialización en Deep Learning. (12 semanas).
- Track de Finanzas Cuantitativas (49 semanas)
- Aplicaciones Financieras De Machine Learning E IA ( 12 semanas).
- Las matemáticas de los mercados financieros (24 semanas).
- Deep Learning for Finance (12 semanas).




