La desigualdad del triángulo en redes neuronales para proteínas
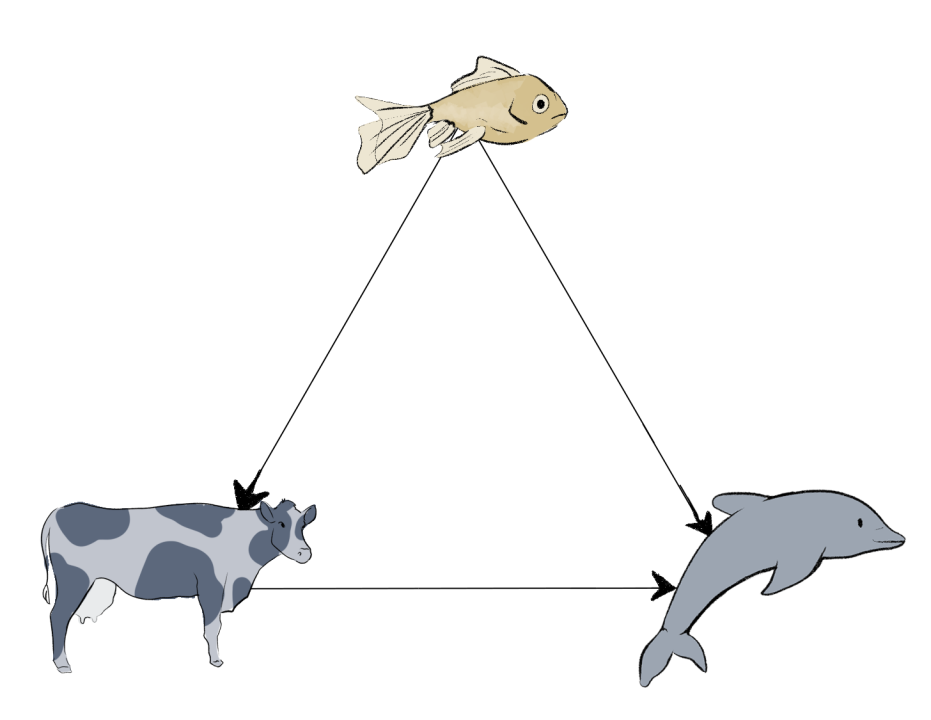
El día de hoy termina nuestro curso de las Lecciones del Colegio de Matemáticas Bourbaki junto a Alvaro de Obeso Fernandez del Valle en este semestre nos hemos dedicado a estudiar AlphaFold y sus profundas implicaciones en la investigación de las Proteínas y sus aplicaciones.
Me gustaría agradecerle a Álvaro lo mucho que nos ha ayudado a entender mejor desde los conceptos más básicos hasta las posibles aplicaciones de estos métodos. También le agradezco mucho a Ángel Pedres quien nos ha ayudado con el desarrollo de algunos ejercicios en Python. Por supuesto felicito a los estudiantes que han participado ya que con sus dudas nos hemos obligado a mejorar la exposición.

Como ya lo he mencionado en otras ediciones de este blog una de las partes fundamentales en el desarrollo de este modelo es el uso de las Graph Neural Networks y en particular el mecanismo de Atención. Sin entrar demasiado en los detalles más técnicos estudiados en el curso me gustaría compartir con toda nuestra comunidad una de las ideas indispensables para que AlphaFold funcione y que al mismo tiempo es uno de los axiomas más importantes para las matemáticas, a saber la desigualdad del triángulo.
Axioma o teorema
Algunas veces escucharemos que la desigualdad del triángulo es un axioma, lo cual no es completamente falso si pensamos en la definición de un espacio métrico, inclusive en e desarrollo de la arquitectura de AlphaFold, la desigualdad del triángulo es un axioma.
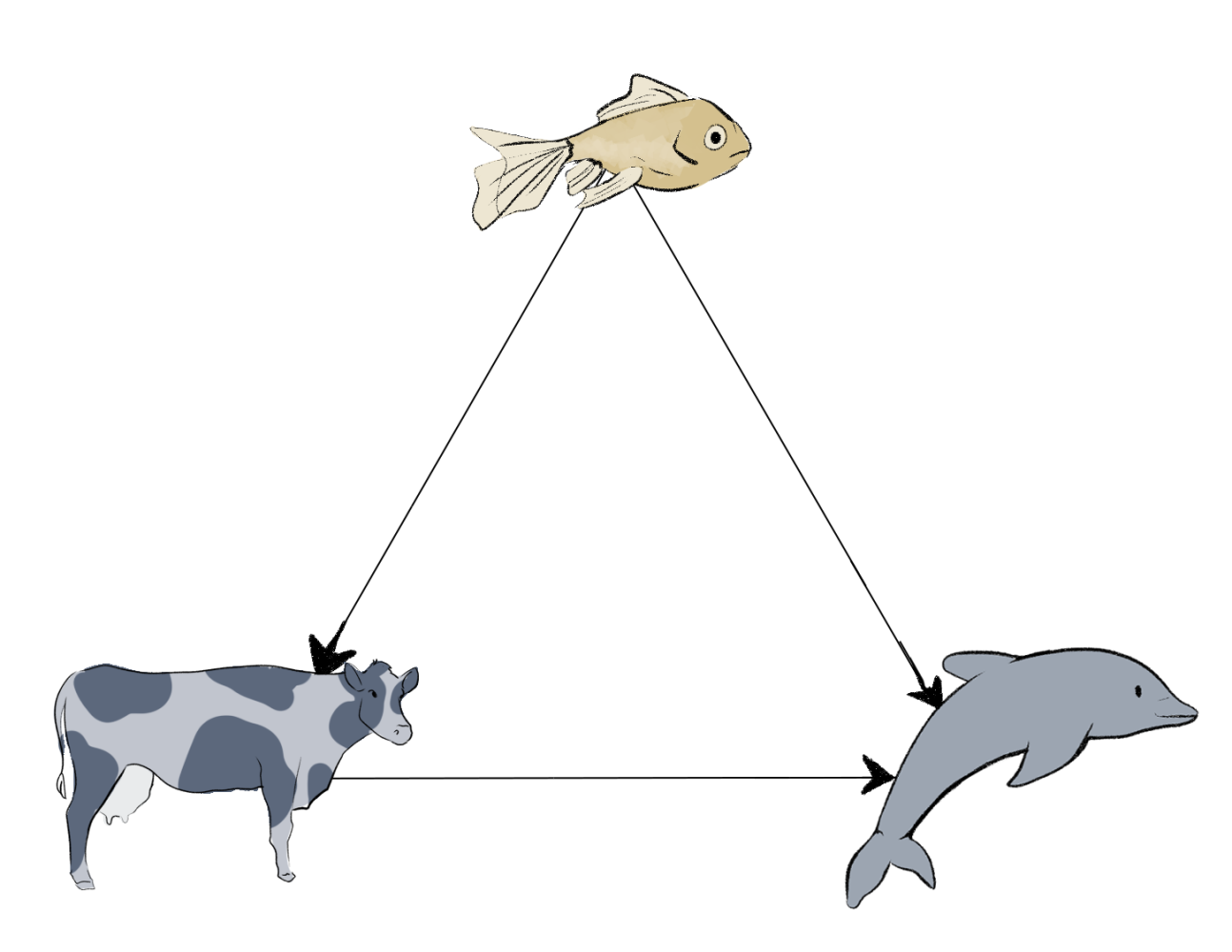
También es cierto que podríamos pensar en la versión más sencilla de la desigualdad del triángulo como un teorema matemático y es lo que haremos para comenzar.
Supongamos que tenemos A, B, C cualesquiera tres números positivos, siempre y cuando estos tres números midan las distancias entre los vértices de un triángulo, se cumplirá la siguiente desigualdad:
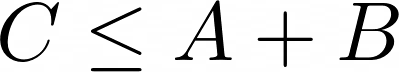
La hipótesis del triángulo sobre estos números es indispensable, evidentemente la desigualdad no es cierta si no se cumple. Una primera observación es que podríamos modificar el orden en el que aparecen los tres números y el resultado es exactamente el mismo.

¡Demostrar este resultado es un ejercicio muy divertido que les recomiendo intentar para relajarse! Les sugiero que me compartan sus demostraciones en los comentarios y el día de mañana yo agregaré algunas ideas.
Triángulos de números, vectores o funciones
El resultado anterior es bastante sencillo y no parece inmediata la relación entre este y las redes neuronales profundas o la estructura cuaternaria de las proteínas.
Para entender mejor cuál es la versión de la desigualdad del triángulo que se utiliza es necesario en lugar de pensar en un punto en el plano como los vértices del triángulo, en un vector de dimensión arbitrariamente grande. Inclusive podríamos pensar en vectores infinitos y este resultado seguiría siendo cierto.
De hecho podríamos modificar nuestra noción intuitiva de distancia (la cual es calculada utilizando el famoso teorema de pitágoras) y definir distancias complicadas entre los vértices de nuestros triángulos generalizados. La desigualdad del triángulo seguirá siendo cierta para otras nociones de distancia.
Triángulos entre aminoácidos
En el caso de AlphaFold y después de un proceso de preprocesamiento de las secuencias de una proteína, podemos pensar cualesquiera tres aminoácidos (o grupos de) determinan distintos triángulos en un espacio de alta dimensión.

La métrica en este caso está determinada por correlaciones estadísticas entre los aminoácidos sin embargo son tantas las características y los registros posibles que es necesario imponer a la desigualdad del triángulo como un axioma en la arquitectura de AlphaFold.
Gracias a lo anterior podemos recuperar un espacio métrico con el cual nos gustaría reproducir el espacio tres dimensional en el que viven las proteínas una vez que haya ocurrido el plegamiento.
Oferta académica del Colegio Bourbaki
- Track de Ciencia de Datos. (49 semanas).
- Machine Learning & AI for the Working Analyst ( 12 semanas).
- Matemáticas para Ciencia de Datos ( 24 semanas).
- Especialización en Deep Learning. (12 semanas).
- Track de Finanzas Cuantitativas (49 semanas)
- Aplicaciones Financieras De Machine Learning E IA ( 12 semanas).
- Las matemáticas de los mercados financieros (24 semanas).
- Deep Learning for Finance (12 semanas).




