Una deducción histórica de las regresiones logísticas


Las regresiones logísticas son uno de los modelos más utilizados en Machine Learning pues aportan un poco de varios mundos: son modelos que permiten un gran número de features gracias a las técnicas de regularización, también son modelos interpretables y al mismo tiempo no son extremadamente pesados en términos computacionales.

En este pequeño artículo vamos a hablar sobre una posible deducción histórica y matemática detrás de las funciones sigmoide en las que se basan las regresiones logísticas.
De ecuaciones diferenciales a la sigmoide
Un enfoque ligeramente distinto para la modelación de fenómenos físicos al que se utiliza en Machine Learning es el de las ecuaciones diferenciales. En este enfoque se propone un modelo matemático que cumpla algunas condiciones sobre la razón de cambio a través del tiempo. Por ejemplo, el crecimiento de una población. Precisamente este fue uno de los problemas más estudiados durante el siglo XIX.
Supongamos que la variable X representa el tiempo y la variable Y representa el crecimiento de una población a medida que X se modifica. El modelo exponencial sugiere la siguiente relación entre X e Y:
La razón de cambio de Y respecto a X es igual a una constante beta multiplicada por el valor actual de Y, es decir:

La razón por la cual se le conoce como modelo exponencial es porque la solución de esta ecuación es lo siguiente, donde Y(0) es el valor inicial de la población.:
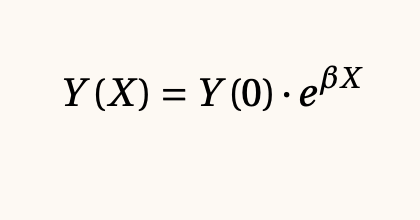
El demógrafo y matemático belga Verhulst, alumno del astrónomo Alphonse Quetelet, propuso una modificación que convierte al modelo exponencial en una versión más realista.

En la vida real, los recursos no son ilimitados, por lo que el crecimiento no puede ser arbitrariamente grande. Por ello, Verhulst consideró una población máxima, a la que llamó K. El modelo modificado tiene la siguiente forma:

En este caso, la razón de cambio del tamaño de la población Y no solo es proporcional a su tamaño actual, sino también a la diferencia entre la población límite K y la población actual. Así, se cumple que el valor de Y(X) está entre 0 y K.
Si interpretamos la población Y(X) como un porcentaje del máximo posible y fijamos K = 1, entonces la ecuación se convierte en:

A esta ecuación le dedicamos la siguiente sección.
Obtención de la función sigmoide

La solución a la ecuación diferencial anterior se puede obtener mediante los siguientes pasos. Comenzamos por despejar beta y sustituir la igualdad:
1 / (Y(X) * (1 - Y(X))) = 1 / Y(X) + 1 / (1 - Y(X))
De este modo, se puede reescribir beta como:
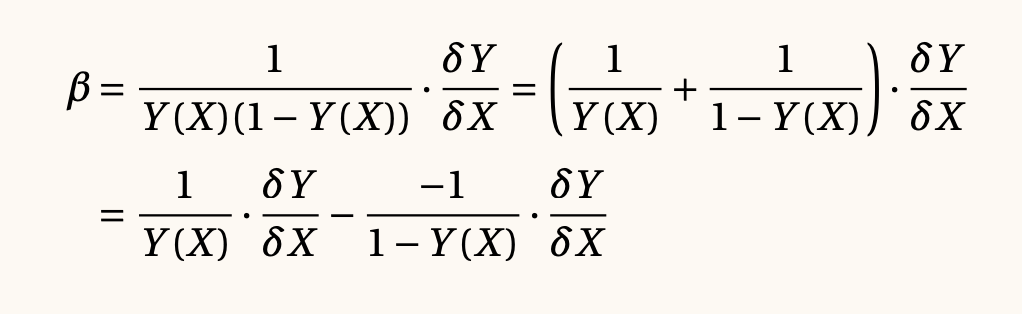
A partir de la definición del logaritmo y de sus derivadas, tenemos las siguientes fórmulas:
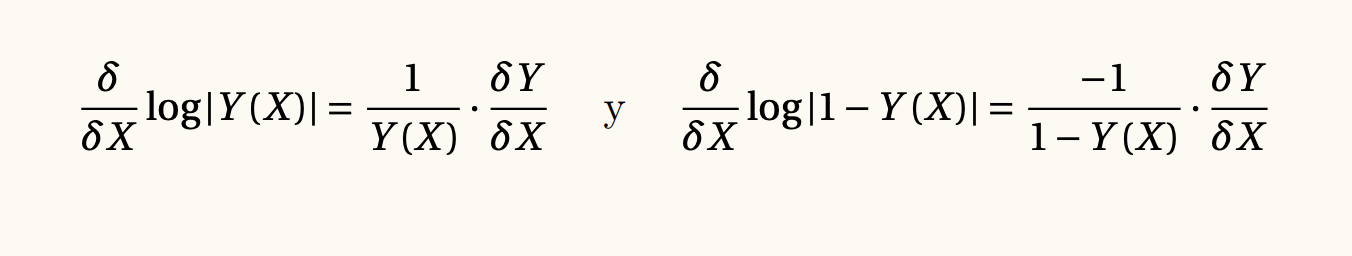
Estamos listos para integrar beta con respecto a X. Dado que Y(X) está entre 0 y 1, podemos omitir los valores absolutos y unificar las constantes de integración en una sola, a la que llamamos C₃. Aplicamos además una propiedad del logaritmo que permite convertir la resta de logaritmos en el logaritmo del cociente:

Aplicamos la función exponencial a ambos lados y luego tomamos el recíproco de la ecuación para despejar Y(X):
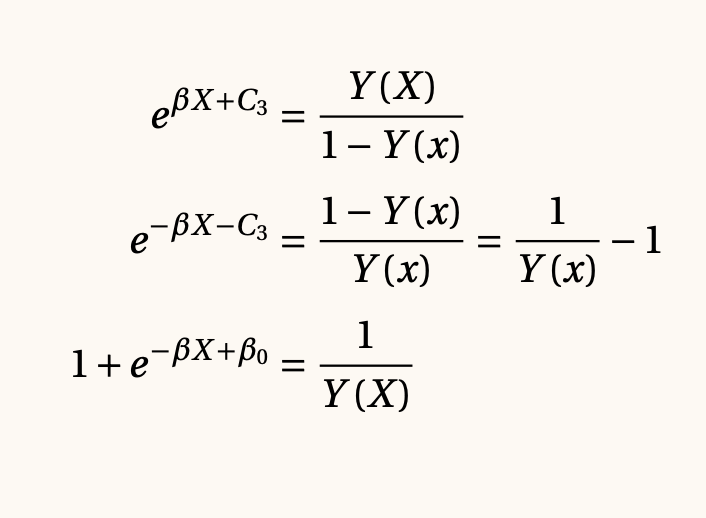
Finalmente, obtenemos la solución esperada. Esta es la fórmula de la función sigmoide, que utilizaremos más adelante para definir la regresión logística:

¿Dónde aprender más sobre machine learning?
En el Colegio de Matemáticas Bourbaki enseñamos con detalle las matemáticas y las bases para que nuestros estudiantes estén listos para aprender los modelos más avanzados de Inteligencia Artificial, Ciencia de Datos y Finanzas Cuantitativas. Estos son los dos cursos que están por comenzar y durarán todo el 2025.
Track de Ciencia de Datos (06 de Mayo 2025, 49 semanas).
Les compartimos algunas notas, presentaciones y clases muestra del curso en el siguiente link.
Aquí pueden asistir virtualmente a la sesión informativa con el Director del Track de Ciencia de Datos. En esta sesión se tratan los conocimientos previos necesarios para inscribirse en nuestro curso, las dinámicas de las clases así como los objetivos finales a los que aspiran nuestros estudiantes al graduarse de este programa.
Track de Ciencia de Finanzas Cuantitativas (05 de Mayo 2025, 49 semanas).
Les compartimos algunas notas, presentaciones y clases muestra del curso en el siguiente link.
Si están interesados en problemas relacionados con Finanzas bursátiles o corporativas podrán asistir virtualmente a la reunión con el director Gerardo Hernandez-del-Valle.





